The LHC experiments put great effort in the preservation of their searches for new physics analysis. This comprises both the publication of expected background yields and their experimentally observed counterparts in HepData.
Further, the exact analysis cut-flows as well as relevant detector efficiencies and resolutions are made publicly available in tools such as Rivet. This puts the community in the advantageous position to reinterpret search data in the light of new physics ideas or generally speaking models that were not considered in the original experimental publication. In principle, all a user needs to do is to generate a signal prediction and confront it with the experimental data and expected background. This is typically done as a hypothesis test that allows to make a judgement about the background only hypothesis or the “signal plus background” hypothesis being more likely. A very convenient measure for this purpose it the so called CLs which is widely used in the LHC programme.
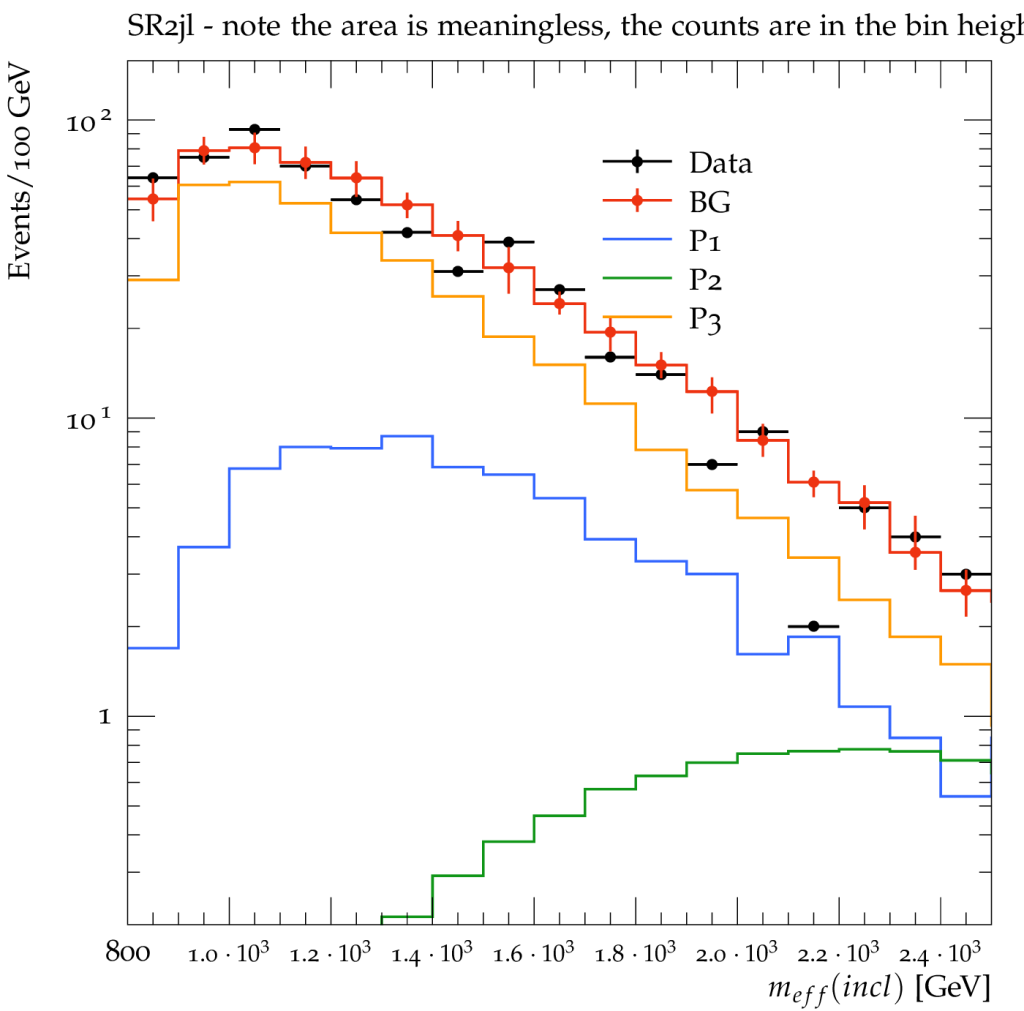
Comparison of ATLAS search data with expected background (BG) and several new physics models. The point P2 yields very few counts and we would not be able to exclude it. The point P3 yields a huge signal and would be excluded.
Typically, new physics models incorporate a number of parameters which affect the signal prediction. In the absence of strong evidence for new physics in the data alone, the task at hand is to at least set limits on model parameters. In the language of CLs that means to find those regions of the model parameter space where the new physics signal prediction is clearly not compatible with the background only hypothesis. From a technical point of view this means evaluating computationally expensive Monte-Carlo event-generators at a multitude of points in the parameter space in question.
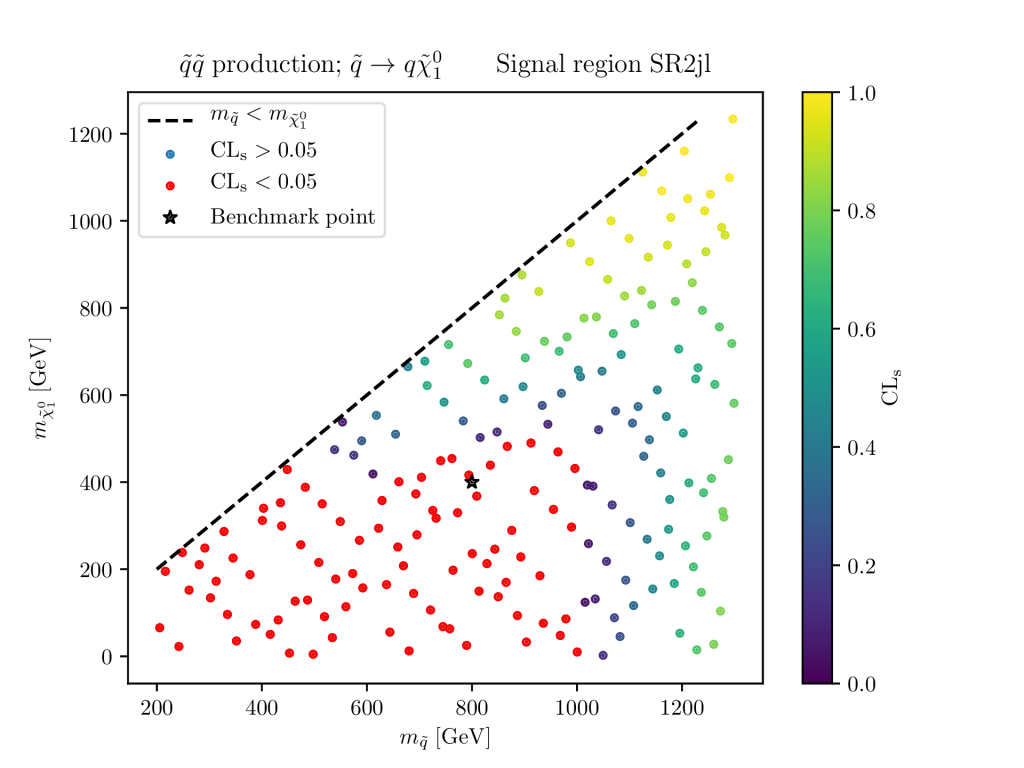
CLs values for 100 exact MC simulations. CPU cost: 100 hours. The excluded parameter region is shown in red.
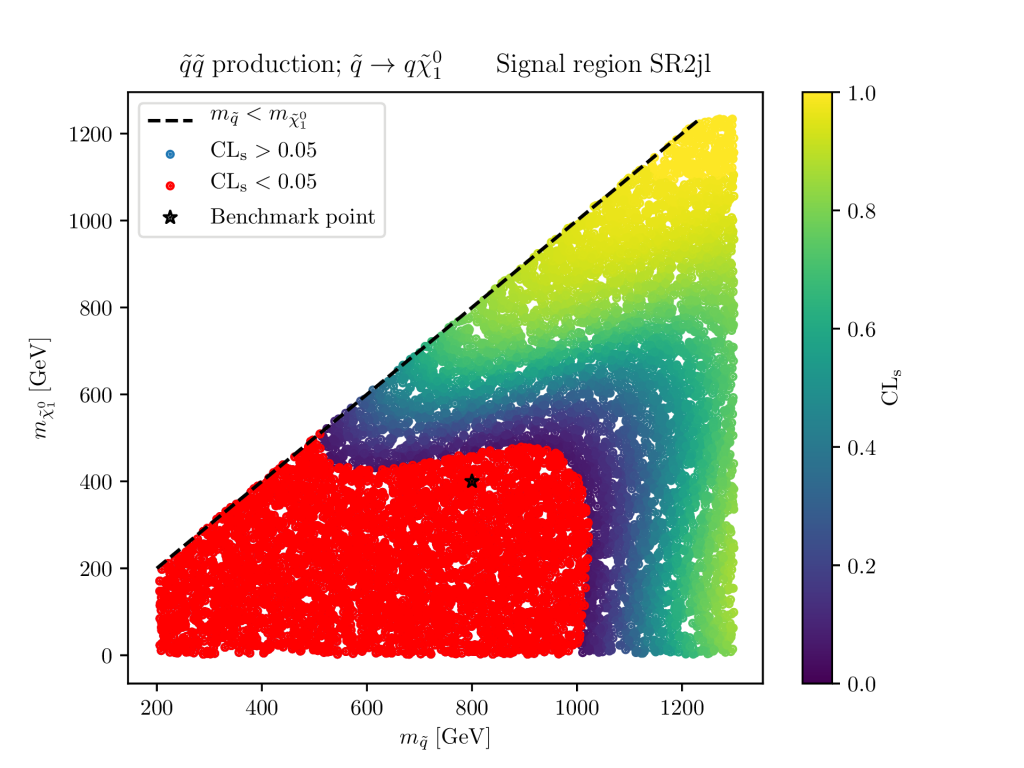
Within scidac we have developed tools that allow to do this task very efficiently. Moreover, by applying rational approximations we are able to reduce the need for exact evaluations of the Monte-Carlos dramatically.
The plot below for example uses the exact Monte Carlos from the plot above to construct rational approximations of the signal prediction. Doing so effectively gives us a fast pseudo-generator that allows to get a very good appriximate signal prediction in milli seconds rather than hours (if compare to the CPU cost of evaluating the full Monte-Carlo). This in turn means that we are able to fill in the white spaces of the plots above for a tiny fraction of what the actual simulation would have cost.
10000 points in the model parameter space obtained with rational approximations. Total CPU cost: 101 hours.